序列模型

序列数据概述

序列数据是指按时间顺序排列的数据，其中每个数据点都依赖于前面的观测值。序列模型的核心是估计条件概率分布：

x_{t} \sim P (x_{t} | x_{t - 1}, \dots, x_{1})

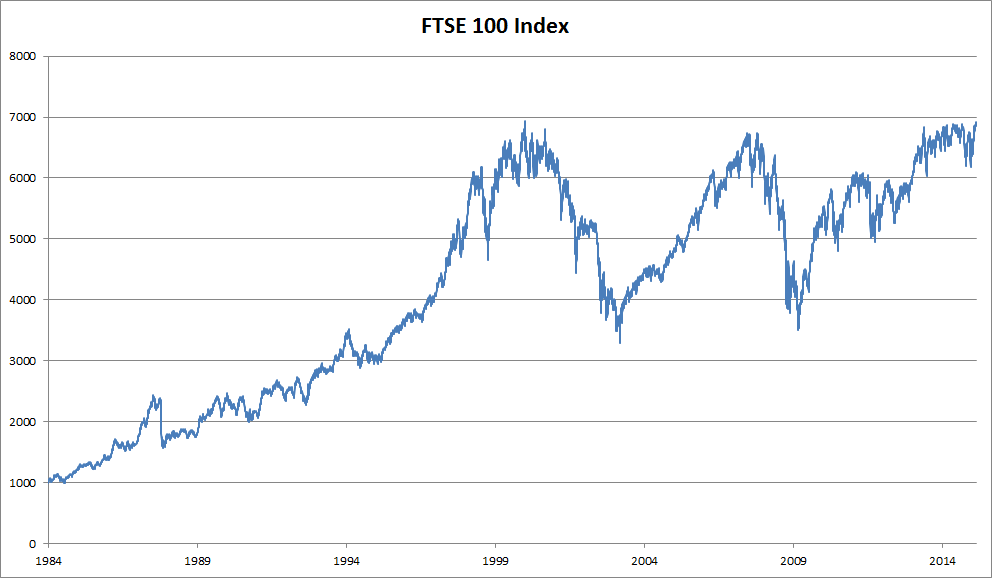
富时100指数

图 1：富时 100 指数 - 典型的序列数据示例

序列数据的特点

时间依赖性：当前观测依赖于历史信息
因果性：未来不能影响过去
非平稳性：数据分布可能随时间变化
预测难度：外推比内插更困难

序列模型的挑战

输入维度变化：历史观测序列长度不固定
误差累积：多步预测中错误会快速积累
计算复杂度：处理长序列计算量大

序列建模策略

自回归模型

基于历史观测值来预测未来值：

P (x_{1}, \dots, x_{T}) = \prod_{t = 1}^{T} P (x_{t} | x_{t - 1}, \dots, x_{1})

两种主要策略：

flowchart TD
    A[序列建模策略] --> B[截断历史]
    A --> C[隐状态建模]

    B --> B1[固定窗口τ]
    B --> B2[马尔可夫假设]

    C --> C1[隐变量h_t]
    C --> C2[递归更新]

    style A fill:#FF4444,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style B fill:#00CCFF,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style C fill:#00FF88,stroke:#FFFFFF,stroke-width:3px,color:#000000
    style B1 fill:#FFB347,stroke:#000000,stroke-width:2px,color:#000000
    style B2 fill:#FFB347,stroke:#000000,stroke-width:2px,color:#000000
    style C1 fill:#98FB98,stroke:#000000,stroke-width:2px,color:#000000
    style C2 fill:#98FB98,stroke:#000000,stroke-width:2px,color:#000000

简单例子：股票价格预测
假设今天股价为 100，昨天为 95，前天为 98
自回归模型： $P (明天价格 | 100, 95, 98, . . .)$
预测明天价格可能为 102 或 97

马尔可夫模型

假设当前状态只依赖于前 τ 个观测：

P (x_{t} | x_{t - 1}, \dots, x_{1}) \approx P (x_{t} | x_{t - τ}, \dots, x_{t - 1})

一阶马尔可夫链：

P (x_{1}, \dots, x_{T}) = \prod_{t = 1}^{T} P (x_{t} | x_{t - 1})

其中 $P (x_{1} | x_{0}) = P (x_{1})$

简单例子：天气预测
状态：{晴天, 雨天, 阴天}
一阶马尔可夫假设：今天天气只依赖昨天
转移概率：
P(今天晴天 | 昨天晴天) = 0.7
P(今天雨天 | 昨天晴天) = 0.2
P(今天阴天 | 昨天晴天) = 0.1
如果昨天是晴天，今天最可能还是晴天

隐变量自回归模型

保持历史信息的总结 $h_{t}$ ：

{\hat{x}}_{t} = P (x_{t} | h_{t})

h_{t} = g (h_{t - 1}, x_{t - 1})

隐变量自回归模型

图 2：隐变量自回归模型架构

简单例子：RNN 语言模型
输入序列：["我", "爱", "学习"]
隐状态更新：
$h_{1} = g (h_{0}, "我")$ → 记住"我"的信息
$h_{2} = g (h_{1}, "爱")$ → 记住"我爱"的信息
$h_{3} = g (h_{2}, "学习")$ → 记住"我爱学习"的信息
预测下一个词： $P (下一词 | h_{3})$ 可能是"编程"、"数学"等

flowchart LR
    x1[我] --> h1[h₁]
    h0[h₀] --> h1
    h1 --> h2[h₂]
    x2[爱] --> h2
    h2 --> h3[h₃]
    x3[学习] --> h3
    h3 --> y[预测：编程]

    style x1 fill:#FF6B6B,stroke:#FFFFFF,stroke-width:2px,color:#FFFFFF
    style x2 fill:#FF6B6B,stroke:#FFFFFF,stroke-width:2px,color:#FFFFFF
    style x3 fill:#FF6B6B,stroke:#FFFFFF,stroke-width:2px,color:#FFFFFF
    style h1 fill:#4ECDC4,stroke:#FFFFFF,stroke-width:2px,color:#FFFFFF
    style h2 fill:#4ECDC4,stroke:#FFFFFF,stroke-width:2px,color:#FFFFFF
    style h3 fill:#4ECDC4,stroke:#FFFFFF,stroke-width:2px,color:#FFFFFF
    style y fill:#FFD93D,stroke:#000000,stroke-width:2px,color:#000000

序列建模的数学基础

三种模型对比

flowchart TD
    A[序列模型对比] --> B[自回归模型]
    A --> C[马尔可夫模型]
    A --> D[隐变量模型]

    B --> B1[使用全部历史]
    B --> B2[计算复杂度高]
    B --> B3[表达能力强]

    C --> C1[固定窗口大小]
    C --> C2[计算简单]
    C --> C3[独立性假设]

    D --> D1[压缩历史信息]
    D --> D2[递归更新]
    D --> D3[平衡复杂度]

    style A fill:#FF1744,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style B fill:#FF9800,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style C fill:#2196F3,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style D fill:#4CAF50,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF

    style B1 fill:#FFE0B2,stroke:#000000,stroke-width:2px,color:#000000
    style B2 fill:#FFE0B2,stroke:#000000,stroke-width:2px,color:#000000
    style B3 fill:#FFE0B2,stroke:#000000,stroke-width:2px,color:#000000

    style C1 fill:#BBDEFB,stroke:#000000,stroke-width:2px,color:#000000
    style C2 fill:#BBDEFB,stroke:#000000,stroke-width:2px,color:#000000
    style C3 fill:#BBDEFB,stroke:#000000,stroke-width:2px,color:#000000

    style D1 fill:#C8E6C9,stroke:#000000,stroke-width:2px,color:#000000
    style D2 fill:#C8E6C9,stroke:#000000,stroke-width:2px,color:#000000
    style D3 fill:#C8E6C9,stroke:#000000,stroke-width:2px,color:#000000

联合概率分解

前向分解：

P (x_{1}, \dots, x_{T}) = \prod_{t = 1}^{T} P (x_{t} | x_{t - 1}, \dots, x_{1})

后向分解：

P (x_{1}, \dots, x_{T}) = \prod_{t = T}^{1} P (x_{t} | x_{t + 1}, \dots, x_{T})

静态性假设

假设序列的动力学规律不随时间改变，即分布是平稳的：

P (x_{t} | x_{t - 1}, \dots, x_{1}) = P (x_{s} | x_{s - 1}, \dots, x_{1}) for all t, s

马尔可夫链的边际化

对于二阶马尔可夫链：

P (x_{t + 1} | x_{t - 1}) = \sum_{x_{t}} P (x_{t + 1} | x_{t}, x_{t - 1}) P (x_{t} | x_{t - 1})

预测方法与挑战

预测类型

flowchart LR
    A[预测方法] --> B[单步预测]
    A --> C[多步预测]

    B --> B1["x̂t+1 = f(xt, ..., xt-τ+1)"]
    C --> C1[逐步预测]
    C --> C2[误差累积]

    style A fill:#9B59B6,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style B fill:#2ECC71,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style C fill:#E74C3C,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style B1 fill:#58D68D,stroke:#000000,stroke-width:2px,color:#000000
    style C1 fill:#F1948A,stroke:#000000,stroke-width:2px,color:#000000
    style C2 fill:#F1948A,stroke:#000000,stroke-width:2px,color:#000000

单步预测公式：

{\hat{x}}_{t + 1} = f (x_{t}, x_{t - 1}, \dots, x_{t - τ + 1})

k 步预测

对于观测序列直到 $x_{t}$ ，k 步预测定义为：

{\hat{x}}_{t + k} = f (x_{t}, x_{t - 1}, \dots, x_{t - τ + 1})

多步预测的递归公式

{\hat{x}}_{605} = f (x_{601}, x_{602}, x_{603}, x_{604})

{\hat{x}}_{606} = f (x_{602}, x_{603}, x_{604}, {\hat{x}}_{605})

{\hat{x}}_{607} = f (x_{603}, x_{604}, {\hat{x}}_{605}, {\hat{x}}_{606})

误差累积问题

假设第一步误差为 $ϵ_{1} = \bar{ϵ}$ ，则：

第二步误差： $ϵ_{2} = \bar{ϵ} + c ϵ_{1}$
误差快速累积，导致长期预测质量下降

误差累积可视化

flowchart LR
    A[真实值] --> B[1步预测]
    B --> C[2步预测]
    C --> D[3步预测]
    D --> E[4步预测]

    A --> A1[x₁ = 10]
    B --> B1[x̂₂ = 10.1<br/>误差=0.1]
    C --> C1[x̂₃ = 10.3<br/>误差=0.3]
    D --> D1[x̂₄ = 10.7<br/>误差=0.7]
    E --> E1[x̂₅ = 11.5<br/>误差=1.5]

    style A fill:#00C851,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style B fill:#FF6D00,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style C fill:#FF6D00,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style D fill:#FF1744,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
    style E fill:#FF1744,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF

总结

时序模型中，当前数据跟之前观察到的数据相关
自回归模型使用自身的过去数据来预测未来
马尔科夫模型假设当前只跟最近少数数据相关，从而简化模型
潜变量模型使用潜变量来概括历史信息
预测方法包括单步预测和多步预测，但多步预测面临误差累积问题

参考资料：D2L 序列模型

序列模型

序列数据概述 #

序列数据的特点 #

序列模型的挑战 #

序列建模策略 #

自回归模型 #

马尔可夫模型 #

隐变量自回归模型 #

序列建模的数学基础 #

三种模型对比 #

联合概率分解 #

静态性假设 #

马尔可夫链的边际化 #

预测方法与挑战 #

预测类型 #

k 步预测 #

多步预测的递归公式 #

误差累积问题 #

误差累积可视化 #

总结 #

序列数据概述

序列数据的特点

序列模型的挑战

序列建模策略

自回归模型

马尔可夫模型

隐变量自回归模型

序列建模的数学基础

三种模型对比

联合概率分解

静态性假设

马尔可夫链的边际化

预测方法与挑战

预测类型

k 步预测

多步预测的递归公式

误差累积问题

误差累积可视化

总结