核心思想
随机抽样一致性算法(Random Sample Consensus)是一种迭代方法,用于从包含离群值的数据中估计数学模型参数。
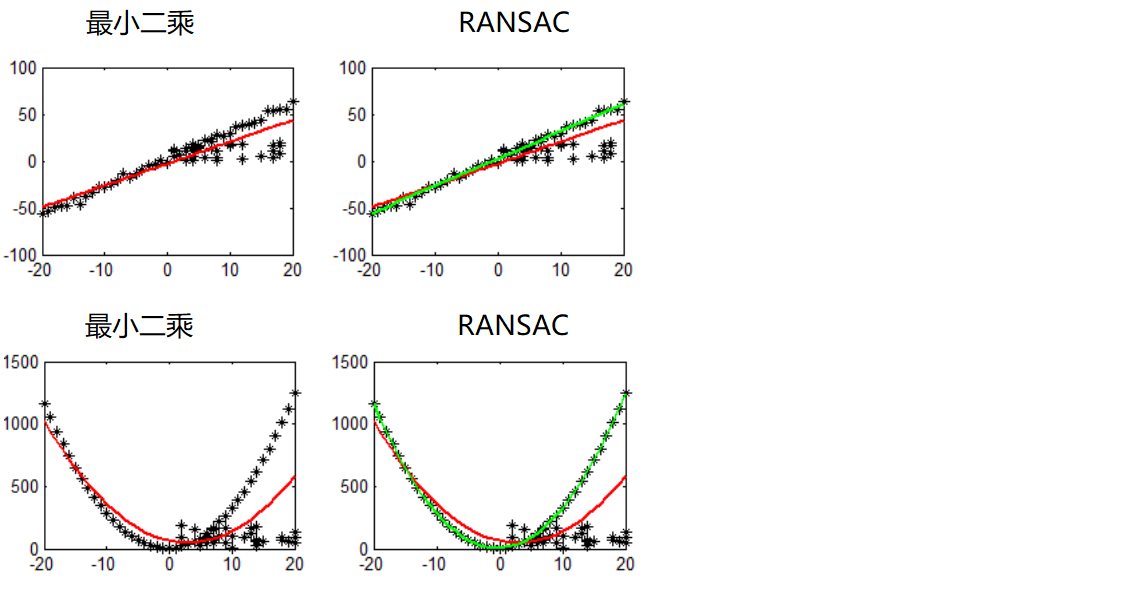
RANSAC 算法的核心思想是:
- 从数据中随机选择最小样本集
- 拟合模型并评估其对所有数据的适用性
- 迭代寻找最佳模型
- 通过内点数量判断模型质量
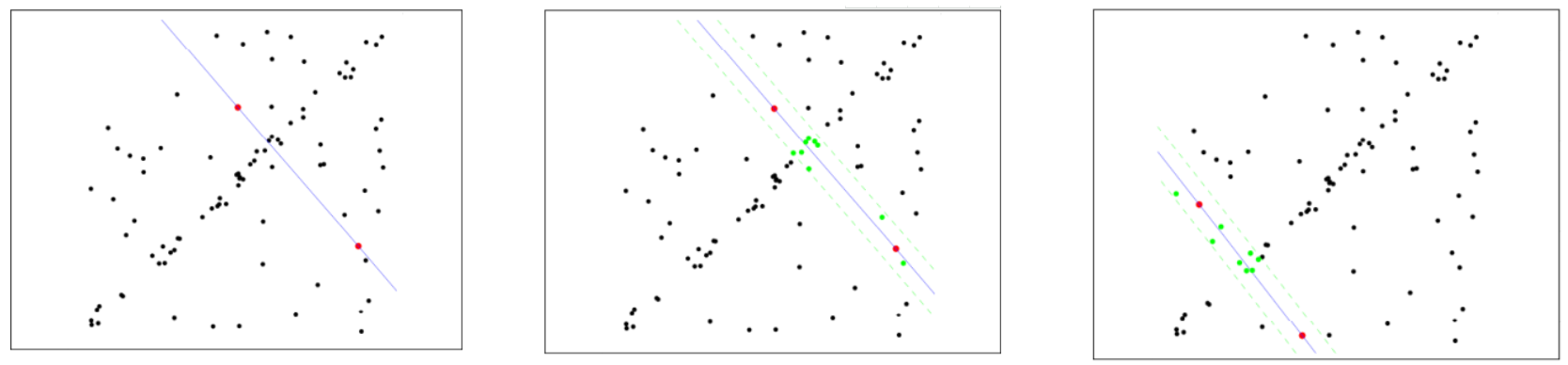
RANSAC 算法步骤
- 随机采样:从数据集中随机选择最小样本集
- 模型拟合:使用最小样本集拟合模型
- 一致性检验:计算所有数据点到模型的距离
- 内点统计:统计误差小于阈值的数据点(内点)
- 迭代优化:重复步骤 1-4,选择内点最多的模型
数学公式
迭代次数估计
其中:
:期望的成功概率(通常取 0.99) :内点比例的估计值 :最小样本集大小
距离阈值
其中:
:常数(通常取 1.96,对应 95%置信度) :噪声标准差
模型评估
对于单应性矩阵估计,重投影误差为:
其中
算法流程图
graph TD
A[输入匹配点对] --> B[设置参数]
B --> C[随机选择样本]
C --> D[拟合模型]
D --> E[计算所有点到模型距离]
E --> F[统计内点个数]
F --> G{是否为最佳模型?}
G -->|是| H[更新最佳模型]
G -->|否| I[记录当前模型]
H --> I
I --> J{达到最大迭代次数?}
J -->|否| C
J -->|是| K[输出最佳模型]
K --> L[使用所有内点重新拟合]
style A fill:#FF3D71,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style B fill:#00D4FF,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style C fill:#00C851,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style D fill:#FF9500,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style E fill:#9C27B0,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style F fill:#E91E63,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style G fill:#FF5722,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style H fill:#4CAF50,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style I fill:#2196F3,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style J fill:#FF9800,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style K fill:#9E9E9E,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
style L fill:#607D8B,stroke:#FFFFFF,stroke-width:3px,color:#FFFFFF
单应性矩阵
单应性矩阵用于描述两个平面之间的投影变换关系:
其中
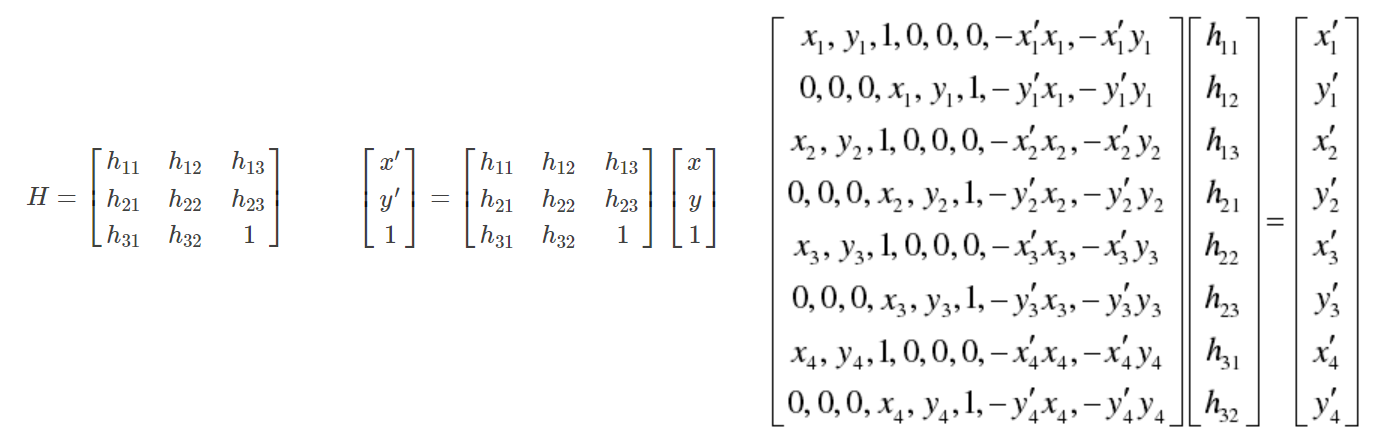
单应性矩阵的物理意义
- 旋转:
项 - 平移:
项 - 透视变换:
项 - 缩放:
项(通常归一化为 1)
变换类型
- 相似变换:旋转、平移、缩放
- 仿射变换:相似变换 + 剪切
- 投影变换:仿射变换 + 透视变换
函数详解
cv2.findHomography(srcPoints, dstPoints, method, ransacReprojThreshold, confidence, maxIters)
参数说明:
srcPoints:源图像特征点,格式为(N, 1, 2)的浮点数组dstPoints:目标图像特征点,格式为(N, 1, 2)的浮点数组method:计算方法
cv2.RANSAC:RANSAC 算法cv2.LMEDS:最小中值算法cv2.RHO:PROSAC 算法ransacReprojThreshold:RANSAC 算法的重投影误差阈值,默认 3.0confidence:置信度,默认 0.99maxIters:最大迭代次数,默认 2000返回值:
homography:3×3 单应性矩阵mask:内点标记数组
cv2.perspectiveTransform(src, m)
参数说明:
src:输入点,格式为(N, 1, 2)的浮点数组m:3×3 变换矩阵返回值:
- 变换后的点坐标
cv2.warpPerspective(src, M, dsize, flags, borderMode, borderValue)
参数说明:
src:输入图像M:3×3 变换矩阵dsize:输出图像大小(width, height)flags:插值方法,默认cv2.INTER_LINEARborderMode:边界处理方式,默认cv2.BORDER_CONSTANTborderValue:边界填充值,默认 0返回值:
- 变换后的图像
基础实现
import cv2
import numpy as np
def ransac_homography_demo():
# 读取图像
img1 = cv2.imread('/images/notes/opencv/box.png', 0)
img2 = cv2.imread('/images/notes/opencv/box_in_scene.png', 0)
# SIFT特征检测
sift = cv2.xfeatures2d.SIFT_create()
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
# 特征匹配
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)
# Lowe's比值测试
good_matches = []
for m, n in matches:
if m.distance < 0.7 * n.distance:
good_matches.append(m)
# 提取匹配点坐标
if len(good_matches) >= 4: # 至少需要4个点来计算单应性矩阵
src_pts = np.float32([kp1[m.queryIdx].pt for m in good_matches]).reshape(-1, 1, 2)
dst_pts = np.float32([kp2[m.trainIdx].pt for m in good_matches]).reshape(-1, 1, 2)
# 使用RANSAC计算单应性矩阵
homography, mask = cv2.findHomography(
src_pts, dst_pts,
cv2.RANSAC,
ransacReprojThreshold=5.0 # 内点阈值
)
# 获取内点匹配
matches_mask = mask.ravel().tolist()
inlier_matches = [good_matches[i] for i in range(len(good_matches)) if matches_mask[i]]
# 绘制匹配结果
img_matches = cv2.drawMatches(
img1, kp1, img2, kp2, inlier_matches, None,
flags=cv2.DrawMatchesFlags_NOT_DRAW_SINGLE_POINTS
)
# 计算图像边界变换
h, w = img1.shape
corners = np.float32([[0, 0], [w, 0], [w, h], [0, h]]).reshape(-1, 1, 2)
transformed_corners = cv2.perspectiveTransform(corners, homography)
# 在目标图像上绘制变换后的边界
img2_with_box = cv2.polylines(
img2.copy(), [np.int32(transformed_corners)],
True, 255, 3, cv2.LINE_AA
)
print(f"总匹配点数: {len(good_matches)}")
print(f"内点数量: {len(inlier_matches)}")
print(f"内点比例: {len(inlier_matches)/len(good_matches):.2%}")
print(f"单应性矩阵:\n{homography}")
return img_matches, img2_with_box, homography
else:
print("匹配点不足,无法计算单应性矩阵")
return None, None, None
# 使用示例
matches_result, box_result, H = ransac_homography_demo()
if matches_result is not None:
cv2.imshow('RANSAC Matches', matches_result)
cv2.imshow('Detected Object', box_result)
cv2.waitKey(0)
cv2.destroyAllWindows()
参数优化
def ransac_with_parameters(img1_path, img2_path, ransac_threshold=5.0, confidence=0.99, max_iters=5000):
"""
带参数的RANSAC单应性矩阵估计
参数:
- ransac_threshold: 内点阈值
- confidence: 置信度
- max_iters: 最大迭代次数
"""
# 读取图像
img1 = cv2.imread(img1_path, 0)
img2 = cv2.imread(img2_path, 0)
# SIFT特征检测
sift = cv2.xfeatures2d.SIFT_create()
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
# 特征匹配
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)
# 筛选好的匹配
good_matches = []
for m, n in matches:
if m.distance < 0.7 * n.distance:
good_matches.append(m)
if len(good_matches) >= 4:
# 提取匹配点坐标
src_pts = np.float32([kp1[m.queryIdx].pt for m in good_matches]).reshape(-1, 1, 2)
dst_pts = np.float32([kp2[m.trainIdx].pt for m in good_matches]).reshape(-1, 1, 2)
# RANSAC参数估计
homography, mask = cv2.findHomography(
src_pts, dst_pts,
method=cv2.RANSAC,
ransacReprojThreshold=ransac_threshold,
confidence=confidence,
maxIters=max_iters
)
# 统计结果
inliers_count = np.sum(mask)
inlier_ratio = inliers_count / len(good_matches)
print(f"RANSAC参数: 阈值={ransac_threshold}, 置信度={confidence}, 最大迭代={max_iters}")
print(f"匹配点数: {len(good_matches)}")
print(f"内点数: {inliers_count}")
print(f"内点比例: {inlier_ratio:.2%}")
return homography, mask, inlier_ratio
return None, None, 0
# 参数测试
test_params = [
{'ransac_threshold': 3.0, 'confidence': 0.95},
{'ransac_threshold': 5.0, 'confidence': 0.99},
{'ransac_threshold': 8.0, 'confidence': 0.999},
]
for params in test_params:
H, mask, ratio = ransac_with_parameters('/images/notes/opencv/box.png', '/images/notes/opencv/box_in_scene.png', **params)
print(f"参数 {params}: 内点比例 {ratio:.2%}")
print("-" * 50)
手动实现 RANSAC
def manual_ransac_homography(src_pts, dst_pts, threshold=5.0, max_iterations=1000, confidence=0.99):
"""
手动实现RANSAC单应性矩阵估计
"""
import random
n_points = len(src_pts)
if n_points < 4:
return None, None
best_homography = None
best_inliers = []
best_score = 0
# 计算所需的迭代次数
sample_size = 4
inlier_ratio_est = 0.5 # 估计内点比例
required_iterations = int(np.log(1 - confidence) / np.log(1 - inlier_ratio_est**sample_size))
iterations = min(max_iterations, required_iterations)
print(f"预计迭代次数: {iterations}")
for i in range(iterations):
# 随机选择4个点
sample_indices = random.sample(range(n_points), sample_size)
sample_src = src_pts[sample_indices]
sample_dst = dst_pts[sample_indices]
# 计算单应性矩阵
try:
H = cv2.getPerspectiveTransform(sample_src.reshape(4, 2), sample_dst.reshape(4, 2))
except:
continue
# 计算所有点的重投影误差
src_homogeneous = np.hstack([src_pts.reshape(-1, 2), np.ones((n_points, 1))])
projected = (H @ src_homogeneous.T).T
projected_2d = projected[:, :2] / projected[:, 2:3]
# 计算误差
errors = np.sqrt(np.sum((projected_2d - dst_pts.reshape(-1, 2))**2, axis=1))
# 统计内点
inliers = errors < threshold
inlier_count = np.sum(inliers)
# 更新最佳模型
if inlier_count > best_score:
best_score = inlier_count
best_homography = H
best_inliers = inliers
# 更新内点比例估计
inlier_ratio_est = inlier_count / n_points
required_iterations = int(np.log(1 - confidence) / np.log(1 - inlier_ratio_est**sample_size))
print(f"迭代 {i+1}: 内点数 {inlier_count}, 内点比例 {inlier_ratio_est:.2%}")
# 使用所有内点重新拟合
if best_score >= 4:
inlier_src = src_pts[best_inliers]
inlier_dst = dst_pts[best_inliers]
if len(inlier_src) >= 4:
refined_H = cv2.findHomography(inlier_src, inlier_dst, cv2.LMEDS)[0]
return refined_H, best_inliers
return best_homography, best_inliers
# 使用示例
def test_manual_ransac():
# 读取图像
img1 = cv2.imread('/images/notes/opencv/box.png', 0)
img2 = cv2.imread('/images/notes/opencv/box_in_scene.png', 0)
# SIFT特征检测
sift = cv2.xfeatures2d.SIFT_create()
kp1, des1 = sift.detectAndCompute(img1, None)
kp2, des2 = sift.detectAndCompute(img2, None)
# 特征匹配
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)
# 筛选好的匹配
good_matches = []
for m, n in matches:
if m.distance < 0.7 * n.distance:
good_matches.append(m)
if len(good_matches) >= 4:
# 提取匹配点坐标
src_pts = np.float32([kp1[m.queryIdx].pt for m in good_matches]).reshape(-1, 1, 2)
dst_pts = np.float32([kp2[m.trainIdx].pt for m in good_matches]).reshape(-1, 1, 2)
# 手动RANSAC
H_manual, inliers_manual = manual_ransac_homography(src_pts, dst_pts)
# OpenCV RANSAC对比
H_opencv, mask_opencv = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)
print(f"手动RANSAC内点数: {np.sum(inliers_manual)}")
print(f"OpenCV RANSAC内点数: {np.sum(mask_opencv)}")
return H_manual, H_opencv, inliers_manual, mask_opencv
return None, None, None, None
# 测试
H_manual, H_opencv, inliers_manual, mask_opencv = test_manual_ransac()
应用场景
1. 图像配准
def image_registration_ransac(img1_path, img2_path):
"""基于RANSAC的图像配准"""
# 读取图像
img1 = cv2.imread(img1_path)
img2 = cv2.imread(img2_path)
# 转换为灰度图
gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)
# SIFT特征检测
sift = cv2.xfeatures2d.SIFT_create()
kp1, des1 = sift.detectAndCompute(gray1, None)
kp2, des2 = sift.detectAndCompute(gray2, None)
# 特征匹配
bf = cv2.BFMatcher()
matches = bf.knnMatch(des1, des2, k=2)
# 筛选好的匹配
good_matches = []
for m, n in matches:
if m.distance < 0.7 * n.distance:
good_matches.append(m)
if len(good_matches) >= 4:
# 提取匹配点
src_pts = np.float32([kp1[m.queryIdx].pt for m in good_matches]).reshape(-1, 1, 2)
dst_pts = np.float32([kp2[m.trainIdx].pt for m in good_matches]).reshape(-1, 1, 2)
# RANSAC估计变换矩阵
M, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)
# 应用变换
h, w, c = img1.shape
registered = cv2.warpPerspective(img1, M, (w, h))
# 计算配准质量
inlier_count = np.sum(mask)
inlier_ratio = inlier_count / len(good_matches)
print(f"配准成功: 内点数 {inlier_count}, 内点比例 {inlier_ratio:.2%}")
return registered, M, inlier_ratio
return None, None, 0
# 使用示例
registered, transform_matrix, quality = image_registration_ransac('/images/notes/opencv/img1.jpg', '/images/notes/opencv/img2.jpg')
if registered is not None:
cv2.imshow('Registered Image', registered)
cv2.waitKey(0)
cv2.destroyAllWindows()
2. 平面检测
def plane_detection_ransac(img_path):
"""基于RANSAC的平面检测"""
# 读取图像
img = cv2.imread(img_path)
gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
# 检测线段
lines = cv2.HoughLinesP(gray, 1, np.pi/180, threshold=100, minLineLength=50, maxLineGap=10)
if lines is not None:
# 使用RANSAC拟合主要平面
points = []
for line in lines:
x1, y1, x2, y2 = line[0]
points.extend([(x1, y1), (x2, y2)])
points = np.array(points)
# 简化的平面拟合(这里用线性拟合代替)
if len(points) >= 2:
# 使用最小二乘法拟合直线
x = points[:, 0]
y = points[:, 1]
A = np.vstack([x, np.ones(len(x))]).T
m, b = np.linalg.lstsq(A, y, rcond=None)[0]
# 计算内点
distances = np.abs(y - (m * x + b)) / np.sqrt(m**2 + 1)
inliers = distances < 10 # 阈值
print(f"检测到 {len(lines)} 条线段")
print(f"内点数: {np.sum(inliers)}")
print(f"主要平面方程: y = {m:.2f}x + {b:.2f}")
# 绘制检测结果
for i, line in enumerate(lines):
x1, y1, x2, y2 = line[0]
color = (0, 255, 0) if inliers[i*2] and inliers[i*2+1] else (0, 0, 255)
cv2.line(img, (x1, y1), (x2, y2), color, 2)
return img
return img
# 使用示例
result = plane_detection_ransac('/images/notes/opencv/building.jpg')
cv2.imshow('Plane Detection', result)
cv2.waitKey(0)
cv2.destroyAllWindows()
3. 异常值检测
def outlier_detection_ransac(points, threshold=2.0):
"""
基于RANSAC的异常值检测
适用于2D点集的直线拟合
"""
n_points = len(points)
if n_points < 2:
return None, None
best_inliers = []
best_score = 0
best_model = None
max_iterations = 1000
for _ in range(max_iterations):
# 随机选择2个点
sample_indices = np.random.choice(n_points, 2, replace=False)
p1, p2 = points[sample_indices]
# 拟合直线 ax + by + c = 0
if p1[0] == p2[0]: # 垂直线
a, b, c = 1, 0, -p1[0]
else:
# y = mx + b => mx - y + b = 0
m = (p2[1] - p1[1]) / (p2[0] - p1[0])
b = p1[1] - m * p1[0]
a, b, c = m, -1, b
# 计算所有点到直线的距离
distances = np.abs(a * points[:, 0] + b * points[:, 1] + c) / np.sqrt(a**2 + b**2)
# 统计内点
inliers = distances < threshold
inlier_count = np.sum(inliers)
if inlier_count > best_score:
best_score = inlier_count
best_inliers = inliers
best_model = (a, b, c)
return best_model, best_inliers
# 使用示例
def test_outlier_detection():
# 生成带噪声的直线数据
np.random.seed(42)
x = np.linspace(0, 10, 50)
y = 2 * x + 1 + np.random.normal(0, 0.5, 50)
# 添加异常值
x = np.append(x, [2, 3, 7, 8])
y = np.append(y, [15, 18, 8, 12])
points = np.column_stack([x, y])
# RANSAC异常值检测
model, inliers = outlier_detection_ransac(points)
if model is not None:
a, b, c = model
print(f"检测到的直线方程: {a:.2f}x + {b:.2f}y + {c:.2f} = 0")
print(f"内点数: {np.sum(inliers)}")
print(f"异常值数: {np.sum(~inliers)}")
# 可视化结果
plt.figure(figsize=(10, 6))
# 绘制内点和异常值
plt.scatter(x[inliers], y[inliers], c='blue', label='内点', alpha=0.7)
plt.scatter(x[~inliers], y[~inliers], c='red', label='异常值', alpha=0.7)
# 绘制拟合直线
x_line = np.linspace(x.min(), x.max(), 100)
if b != 0:
y_line = -(a * x_line + c) / b
plt.plot(x_line, y_line, 'g-', label='RANSAC拟合直线', linewidth=2)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('RANSAC异常值检测')
plt.legend()
plt.grid(True, alpha=0.3)
plt.show()
# 测试
test_outlier_detection()
优化技巧
1. 自适应阈值
def adaptive_threshold_ransac(src_pts, dst_pts, initial_threshold=5.0):
"""自适应阈值RANSAC"""
current_threshold = initial_threshold
best_homography = None
best_inliers = []
thresholds = [initial_threshold * 0.5, initial_threshold, initial_threshold * 2.0]
for threshold in thresholds:
H, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, threshold)
if H is not None:
inlier_count = np.sum(mask)
inlier_ratio = inlier_count / len(src_pts)
print(f"阈值 {threshold}: 内点数 {inlier_count}, 内点比例 {inlier_ratio:.2%}")
if len(best_inliers) == 0 or inlier_count > len(best_inliers):
best_homography = H
best_inliers = mask
current_threshold = threshold
return best_homography, best_inliers, current_threshold
2. 多模型 RANSAC
def multi_model_ransac(src_pts, dst_pts, models=['homography', 'affine']):
"""多模型RANSAC"""
results = {}
for model_type in models:
if model_type == 'homography':
if len(src_pts) >= 4:
H, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)
results[model_type] = {
'matrix': H,
'inliers': mask,
'inlier_count': np.sum(mask) if mask is not None else 0
}
elif model_type == 'affine':
if len(src_pts) >= 3:
# 仿射变换需要至少3个点
A = cv2.estimateAffinePartial2D(src_pts, dst_pts, method=cv2.RANSAC)[0]
# 简化处理,实际应用中需要计算内点
results[model_type] = {
'matrix': A,
'inliers': None,
'inlier_count': 0
}
# 选择最佳模型
best_model = max(results.keys(), key=lambda k: results[k]['inlier_count'])
return results, best_model
性能分析
参数对性能的影响
阈值:
- 过小:内点数减少,可能错过正确模型
- 过大:异常值被误判为内点
最大迭代次数:
- 过小:可能找不到最优解
- 过大:计算时间增加
置信度:
- 影响所需的迭代次数
- 高置信度需要更多迭代
复杂度分析
- 时间复杂度:O(k × n),其中 k 是迭代次数,n 是数据点数
- 空间复杂度:O(n)
- 实际迭代次数:依赖于内点比例和所需置信度
优缺点
优点
- 鲁棒性强:能够处理大量异常值
- 通用性好:适用于各种模型拟合
- 实现简单:算法逻辑清晰
- 效果稳定:在噪声环境下表现良好
缺点
- 计算量大:需要多次迭代
- 参数敏感:阈值选择影响结果
- 随机性:结果可能有轻微变化
- 不适用于内点比例很低的情况
应用领域
- 计算机视觉:图像配准、物体识别
- 机器人学:SLAM、路径规划
- 医学影像:图像配准、病变检测
- 遥感:地图匹配、变化检测
- 三维重建:点云配准、结构恢复
实用技巧
1. 参数选择策略
def optimize_ransac_params(src_pts, dst_pts):
"""RANSAC参数优化策略"""
n_matches = len(src_pts)
# 根据匹配点数量调整参数
if n_matches < 20:
threshold = 3.0
confidence = 0.95
max_iters = 1000
elif n_matches < 50:
threshold = 5.0
confidence = 0.99
max_iters = 2000
else:
threshold = 8.0
confidence = 0.999
max_iters = 5000
# 根据图像大小调整阈值
img_diagonal = np.sqrt(640**2 + 480**2) # 假设图像大小
adaptive_threshold = threshold * (img_diagonal / 800)
return adaptive_threshold, confidence, max_iters
2. 质量评估
def evaluate_homography_quality(H, src_pts, dst_pts):
"""评估单应性矩阵质量"""
if H is None:
return {'valid': False}
# 计算重投影误差
src_homogeneous = np.hstack([src_pts.reshape(-1, 2), np.ones((len(src_pts), 1))])
projected = (H @ src_homogeneous.T).T
projected_2d = projected[:, :2] / projected[:, 2:3]
errors = np.sqrt(np.sum((projected_2d - dst_pts.reshape(-1, 2))**2, axis=1))
# 质量指标
mean_error = np.mean(errors)
std_error = np.std(errors)
max_error = np.max(errors)
# 条件数检查
condition_number = np.linalg.cond(H)
return {
'valid': True,
'mean_error': mean_error,
'std_error': std_error,
'max_error': max_error,
'condition_number': condition_number,
'is_stable': condition_number < 1000
}
3. 多尺度 RANSAC
def multi_scale_ransac(img1, img2, scales=[1.0, 0.5, 0.25]):
"""多尺度RANSAC提高鲁棒性"""
best_H = None
best_inliers = 0
for scale in scales:
# 缩放图像
h1, w1 = img1.shape[:2]
h2, w2 = img2.shape[:2]
scaled_img1 = cv2.resize(img1, (int(w1*scale), int(h1*scale)))
scaled_img2 = cv2.resize(img2, (int(w2*scale), int(h2*scale)))
# 在缩放图像上进行RANSAC
H_scaled, inliers = perform_ransac(scaled_img1, scaled_img2)
if H_scaled is not None:
# 将变换矩阵转换回原始尺度
S = np.array([[1/scale, 0, 0], [0, 1/scale, 0], [0, 0, 1]])
H_original = S @ H_scaled @ np.linalg.inv(S)
# 在原始尺度上验证
inlier_count = validate_homography(H_original, img1, img2)
if inlier_count > best_inliers:
best_H = H_original
best_inliers = inlier_count
return best_H, best_inliers
4. 渐进式 RANSAC
def progressive_ransac(src_pts, dst_pts, initial_threshold=5.0, reduction_factor=0.8):
"""渐进式RANSAC:逐步减小阈值"""
current_threshold = initial_threshold
best_H = None
best_inliers = []
while current_threshold > 1.0:
H, mask = cv2.findHomography(
src_pts, dst_pts,
cv2.RANSAC,
current_threshold,
maxIters=1000
)
if H is not None:
inlier_count = np.sum(mask)
if len(best_inliers) == 0 or inlier_count >= len(best_inliers) * 0.8:
best_H = H
best_inliers = mask
# 用更小的阈值继续优化
current_threshold *= reduction_factor
else:
break
else:
break
return best_H, best_inliers
常见问题
Q1: RANSAC 结果不稳定怎么办?
A1: 结果不稳定的原因和解决方案:
def stable_ransac(src_pts, dst_pts, num_runs=5):
"""多次运行RANSAC取最稳定结果"""
results = []
for _ in range(num_runs):
H, mask = cv2.findHomography(src_pts, dst_pts, cv2.RANSAC, 5.0)
if H is not None:
inlier_count = np.sum(mask)
results.append((H, mask, inlier_count))
if not results:
return None, None
# 选择内点数最多的结果
best_result = max(results, key=lambda x: x[2])
return best_result[0], best_result[1]
Q2: 如何处理匹配点数量不足的情况?
A2: 匹配点不足的处理策略:
def handle_insufficient_matches(matches, min_matches=10):
"""处理匹配点不足的情况"""
if len(matches) < min_matches:
print(f"警告:匹配点数量不足({len(matches)} < {min_matches})")
# 策略1:降低匹配阈值
# 重新进行更宽松的匹配
# 策略2:使用其他特征检测器
# 尝试ORB、AKAZE等其他算法
# 策略3:调整图像预处理
# 增强对比度、直方图均衡化等
return False
return True
Q3: 如何优化 RANSAC 的计算速度?
A3: 性能优化策略:
def fast_ransac(src_pts, dst_pts):
"""快速RANSAC实现"""
# 策略1:预筛选匹配点
if len(src_pts) > 100:
# 使用距离阈值预筛选
good_matches = prefilter_matches(src_pts, dst_pts)
src_pts = src_pts[good_matches]
dst_pts = dst_pts[good_matches]
# 策略2:自适应迭代次数
max_iters = min(2000, len(src_pts) * 10)
# 策略3:早停机制
H, mask = cv2.findHomography(
src_pts, dst_pts,
cv2.RANSAC,
ransacReprojThreshold=5.0,
maxIters=max_iters,
confidence=0.99
)
return H, mask
Q4: 如何判断 RANSAC 结果的可靠性?
A4: 可靠性评估方法:
def assess_ransac_reliability(H, mask, src_pts, dst_pts):
"""评估RANSAC结果可靠性"""
if H is None or mask is None:
return {'reliable': False, 'reason': 'No valid homography found'}
inlier_count = np.sum(mask)
total_matches = len(src_pts)
inlier_ratio = inlier_count / total_matches
# 可靠性检查
checks = {
'sufficient_inliers': inlier_count >= 8,
'good_inlier_ratio': inlier_ratio >= 0.2,
'stable_matrix': np.linalg.cond(H) < 1000,
'reasonable_transform': check_transform_reasonableness(H)
}
reliable = all(checks.values())
return {
'reliable': reliable,
'inlier_count': inlier_count,
'inlier_ratio': inlier_ratio,
'condition_number': np.linalg.cond(H),
'checks': checks
}
Q5: 如何处理图像旋转角度过大的情况?
A5: 大角度旋转处理:
def robust_ransac_rotation(img1, img2, max_rotation=45):
"""处理大角度旋转的鲁棒RANSAC"""
# 尝试不同的旋转角度
angles = np.arange(-max_rotation, max_rotation+1, 15)
best_H = None
best_inliers = 0
for angle in angles:
# 旋转第一幅图像
center = (img1.shape[1]//2, img1.shape[0]//2)
rotation_matrix = cv2.getRotationMatrix2D(center, angle, 1.0)
rotated_img1 = cv2.warpAffine(img1, rotation_matrix, (img1.shape[1], img1.shape[0]))
# 在旋转后的图像上进行RANSAC
H, inliers = perform_ransac(rotated_img1, img2)
if H is not None and inliers > best_inliers:
# 补偿旋转
rotation_3x3 = np.eye(3)
rotation_3x3[:2, :2] = rotation_matrix[:2, :2]
rotation_3x3[:2, 2] = rotation_matrix[:2, 2]
compensated_H = H @ rotation_3x3
best_H = compensated_H
best_inliers = inliers
return best_H, best_inliers